Grover算法是量子计算领域的主要算法之一。在处理从无序的D个数据库中搜索M个目标数这一问题时，它优于最好的经典算法可做平方加速。也就是说，经典算法完成任务所需的时间正比于，而量子算法则可在时间尺度内实现。如果D是一个非常大的数字，这将极大地节约时间。Grover算法的强大在于它的多功能性：它的公式是通用的，可适用于很多问题，比如：密码学、矩阵和图形问题、优化以及量子机器学习等。
尽管发现至今已有二十多年，但Grover算法的基本公式一直没变。该算法的最初版本中，首先制备全部量子态的叠加态（状态），然后循环进行操作使得目标态的符号反向(Oracle算符)且态的符号也反向(Grover算符)。在执行次操作后，量子态被旋转至目标态。Grover算法的公式没有改变的原因在于，因为初始算法在时间尺度上已经是最优的，不太可能找到一个更好的算法可从无序的数据库D中找到给定的M个目标数。
当时间尺度最优时，这并不意味着该算法总是有利于实现。比如，执行Grover算符需要对唯一的量子态做相位反转，这通常需要一个尺度正比于比特数平方的算法，实际实现起来可能困难。另外，该算法在运算中并不对称，Oracle算符中M个目标态的符号是反向的，而Grover算符中仅一个状态是反向的。为什么会这样？
Tim Byrnes教授和两个学生Louis Tessler和Gary Forster研究了这些问题，并首次推广了Grover算法，以致于Grover算符使N个量子态的符号反向，Oracle算符使M个量子态的符号反向。这是Grover算法的第一项重要推广，可以通过理解由图1所示的能级结构对应的哈密顿量来实现（如图1）。这导致他们进行了第二个有趣的研究，Grover算法根本不需要解决数据库问题。研究能级结构揭示，利用量子相位估计解决Grover问题完全绕过了Grover迭代。分析时间尺度表明，平均来说可获得非常接近于原始Grover算法的最优时间。由于这两个突破，相关结果发表在Phys. Rev. Lett. 120, 060501 (2018).
结果的主要影响是双重的。首先，Grover算符的推广应该能使Grover算法在唯一量子态很难反向的系统中实现。分析表明，即使对量子态的控制有限，也能以更一般的方法来实现Grover算法。这可能包括很难操控单个粒子的连续变量和高维自旋系统。其次，他们证明了量子相位估计在解决数据库搜索问题上是相当强大的。考虑到量子相位估计在其它量子线路中的巨大效用，它作为许多量子问题的子程序的重要性得到显著提高。
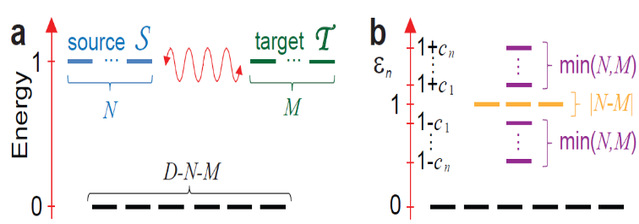
图1 (a) 源态和靶态的拉比共振作为Grover算法演化的示意图； (b) Grover哈密顿量的能级结构。
PhysRevLett.120.060501(2018).pdf
