We report on a high-speed temporal and spatial multiplexed single-photon counter with photon-number-resolving capability up to four photons. The infrared detector combines a fiber loop to split, delay and recombine optical pulses and a 200 MHz dual-channel single-photon detector based on InGaAs/InP avalanche photodiode. To fully characterize the photon-number-resolving capability, we perform quantum detector tomography and then reconstruct its positive-operator-valued measure and the associated Wigner functions. The result shows that, despite of the afterpulsing noise and limited system detection efficiency, this temporal and spatial multiplexed single-photon counter can already find applications for large repetition rate quantum information schemes.
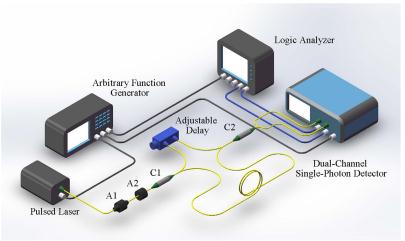
Figure 1. Experimental setup. The pulsed laser at 1550nm is operated with a repetition rate of 10MHz. It is strongly attenuated to be used as QDT probe. The delay between the two paths in the fiber loop is adjusted to be 50ns. The dual-channel single-photon detector based on InGaAs/InP APD is operated at 200MHz, and the self-differencing technique is used to suppress the spike noise induced by the gating pulse. The outputs of the detector are recorded by the logic analyzer. The synchronization of the whole system is provided by the arbitrary function generator. A1: adjustable attenuator; A2: fixed attenuator; C1 and C2: 50/50 fiber beam-splitters.
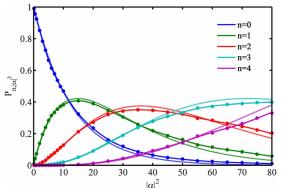
Figure 2. Experimental data. The plots provide the probability of the different detector outcomes as a function of the average photon number |α| 2 of the weak coherent probe pulses. The points correspond to the experimental data while the solid and dotted lines provide the results of the tomography and the theoretical simulation respectively. (blue for n=0, green for n=1, red for n=2, cyan for n=3, purple for n=4).
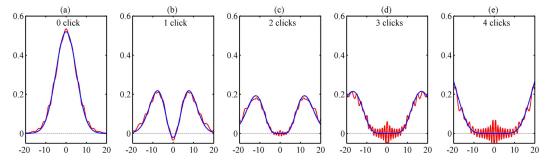
Figure 3. (a–e) Cross section of the experimental Wigner functions obtained from the reconstructed POVM elements for 0 to 4 clicks outcomes. The red and blue lines provide the experimental Wigner function and the theoretical simulation respectively. Note that all the Wigner functions are normalized between −1 and 1.

